Baldur's Gate II: Shadows of Algebra
A genie takes you back to school
I used to play my fair share of cRPGs when I was younger, and the Infinity Engine-powered Dungeons & Dragons ones were certainly some of my favorites. I loved going back to the giant tree/town of Kuldahar in Icewind Dale as warm respite from wintery spelunking and slaying of undead hordes, and if you ever ask me about my all-time top video games Planescape: Torment is sure to come up on the short-shortlist. In fact, last month at my dear friend’s (socially-distanced!) wedding I learned that several years prior I had apparently convinced1 the groom’s brother to play through Planescape: Torment and it had since become his favorite game. I also happened to learn that Baldur’s Gate III is set to release soon, which reminded me that despite my affinity for its cousins I never played through any Baldur’s Gate games for which the Infinity Engine was originally built. Here in the times of COVID and punishing west coast fires, I smelled an opportunity for me to play what has been hailed as one of the (if not the) D&D cRPGs of all time, Baldur’s Gate II: Shadows of Amn.
Hours of character build research and one somewhat long and bland tutorial dungeon later, I found myself in the city of Athkatla. Returning to the, uh, quirky2 “Advanced” D&D rules and 2000 graphics and UI had been a jolt of uneasy nostalgia, but now I was in an area teeming with life I was excited. I found a little boy in distress because his mother went into the circus tent and hadn’t come back (“Stay here, son. I’m definitely not abandoning you here to join the circus. That would be crazy and irresponsible.” ;) ). Perfect! My first side quest. Straight into the circus tent my party went and there I got another flashback to the early 2000s, this time in the form of an algebra problem from a genie barring my path, Monty Python style.
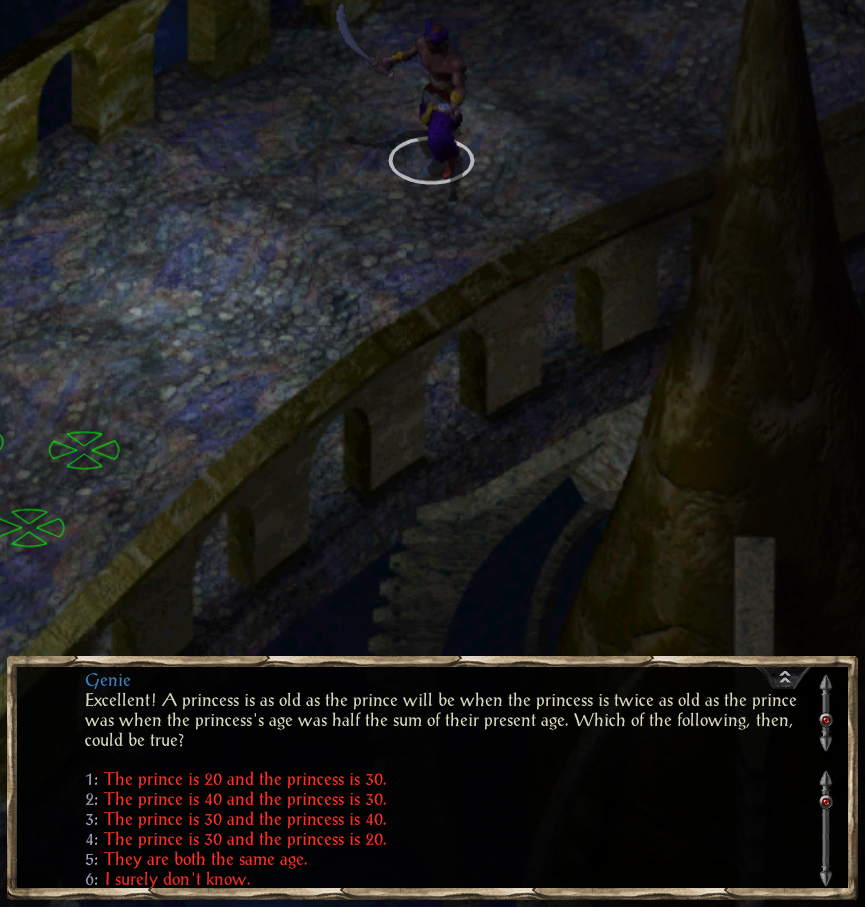
Thank you Beamdog for bringing these blurry 2000 graphics to my 2019 MacBook Pro with Retina Display
A princess is as old as the prince will be when the princess is twice as old as the prince was when the princess’s age was half the sum of their present age. Which of the following, then, could be true?
- The prince is 20 and the princess is 30.
- The prince is 40 and the princess is 30.
- The prince is 30 and the princess is 40.
- The prince is 30 and the princess is 20.
- They are both the same age.
Now, given how fast it is to reload a saved game, the easiest way to find out the right answer is surely to just try them all and earn the sweet, sweet experience points. But that’s no fun! I’m a reasonably intelligent person so I should be able to figure this out…right? Challenge accepted!
Algebraic!
I stared at the riddle, thinking I should just should be able to muse out loud and find the answer. I couldn’t wrap my head around it though - the edges of the puzzle were too slippery. An epiphany! I simply needed create some equations and solve for their age and it would be easy. I stared back at the problem. I was having trouble parsing the English. Diffidence and determination crept in. How could I even create equations for this if I couldn’t even understand the problem? I struggled to break it down but after much head scratching I managed to string some ideas together:
# > when the princess's age was half the sum of their present age
# Aha! The age of the princess previously
1. princess_past = (princess_now + prince_now) / 2
# > when the princess is twice as old as the prince was
2. princess_fut = prince_past * 2
# > A princess is as old as the prince will be
3. princess_now = prince_fut
# We don't have any anchoring ages, but we know there is a consistent difference between their ages
4. prince_fut = princess_fut + x
5. prince_past = princess_past + x
6. prince_now = princess_now + x
# That was the hard part. Now let's mix up some of the variables! Use 6. in 1.
7. princess_past = (princess_now + [princess_now + x])/2
# Use 7. in 5.
8. prince_past = (princess_now + princess_now + x)/2 + x
# That's ugly. Let's multiply both sides by 2 and clean it up.
9. 2 * prince_past = (2 * princess_now) + 3x
# Use 2.
10. princess_fut = 2 * princess_now + 3x
# Use 4.
11. prince_fut - x = 2 * princess_now + 3x
12. prince_fut = 2 * princess_now + 4x
# Use 3.
13. princess_now = 2 * princess_now + 4x
# Excellent! Now we can relate princess_now and x
14. -princess_now = 4x
# From 6.
15. prince_now - princess_now = x
# 14. and 15 to express everything in terms of "now" values
16. -princess_now = 4 * prince_now - 4 * princess_now
# Let's get those ratios!
17. 3 * princess_now = 4 * prince_now
# Even better, let's get a conversion
18. princess_now = (4/3) * prince_now
So the answer must be
- The prince is 30 and the princess is 40.
Something tells me my sorcerer didn’t pause to pull out a pen and paper like I did, so while this perhaps broke the immersion it also led to a pretty satisfying experience. That being said, I have a hard time imagining this counted favorably towards it being such highly-rated game, so I’m eagerly anticipating what other surprises the game has in store for me.
Have you had any other fun experiences with algebra lately? Excited for Baldur’s Gate III? Want to extol the virtues of your favorite D&D game? Leave a comment!
-
A Planescape: Torment mini-pitch: after being presumed dead, you amnesically wake up in a mortuary to a floating skull who reads your fully-tatooed back to you to jog your memory. Over the course of your adventure, you discover what you’ve done prior to your “death” and recruit a retinue including a succubus who owns a brothel where only intellectual lusts are pursued, a pyromaniac mage who has set himself on fire permanently, and a robot who has gone rogue and been rejected from his race’s hive-mind due to overexposure to chaos. Nearly all of the game is completable without engaging in combat and the storytelling and zany world-building is so fantastic that many “non-gamers” can appreciate it. ↩︎
-
Who thought THAC0 - “to hit armor class 0” - and a less-is-better, ideally negative score for your armor were good design ideas? ↩︎

Share this post
Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email